有名実践だからこそ工夫をして
4年生に授業をしてみましたので,映像を撮ってサークルで検討していただきました。
授業の概要は以下の通りでした。
(1)○を板書し,線を1本ひいて分けると,2つに分かれることを伝える。
(2)線を2本ひくとどうなるか問う。しばらくして,指名する。
「×」のようにひいて4つに分かれるという答えが出される。
(3)他に方法はないか問う。
「=」のようにひいて3つに分かれるという答えが出される。
(4)答えは一つではなく幾通りかあることを確認しする。
(5)線を3本ひくとどうなるか問う。
しばらく考える時間を与え,できた子を指名して答えを確認する。

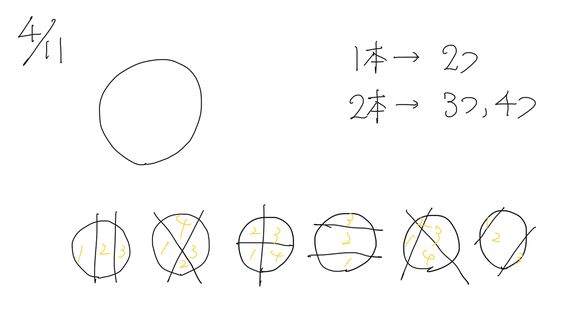
例えば,左から2番めと左から5番目は同じ4つですが,分け方が違うと考えている子供ももいます。だから,いったんいろいろ出させて確認していく必要があります。その時も,「これとこれは同じです。」と確認しては面白くありません。例えば,左から5番目はなどは大変ユニークで,「これは間違っているね」と言って「先生合っています。」などとやり取りをしてもよいのではないかと思うのです。
山場となるところは大いに工夫して
この授業の山場は次に3本線をひいていくつ分かれるかというところにあります。2本ひいた時に,答えは一通りではないと確認していますので,何通りか考えられます。答えは,4つ,5つ,6つ,7つと4通りあります。

普通なら,「できた人」と聞き,挙手した児童を指名。正解か不正解かを教師が伝えて,一つ一つ答え合わせをしていくでしょう。しかし,それでは淡々と進みすぎて面白くない。
では,どうしたら盛り上がるでしょうか。
(少し考えてみてください。)
できた児童にノートを持ってこさせ,確認をします。おそらく,ほとんどの児童が2通りか3通り書いて持ってくるでしょう。
ノートを持ってきた児童を,教室の前に並べていきます。おそらく,算数が得意な子が並ぶはずです。そこで一気に畳み掛けます。
「全員不正解です。」
おそらく,
「えーっ。」「何で?。」となるはずです。
そして,さらに自分で考えたり,友達と相談したりして答えを見つけようとします。解けたときの達成感もかなりのものになると思いました。
向山型算数の基本である,黙ってノートにバツをつけることで,子供はさらに考え始めるという原則を思い出しました。
これは,絶対に盛り上がるという確信があります。ぜひ,実践したいと思いました。
文章では分からないことがある
書籍や論文を読んで追試しても盛り上がる時と盛り上がらない時があります。そんな時,「実践が悪い。」「子供が悪い。」と考えてしまっては成長がありません。しかし,自分のどこが足りないのか自分で見つけるのはなかなか難しいです。
そんな時に,授業の様子を映像にとって客観的に見るとヒントがあります。さらに,サークルで見てもらうことで,自分の視点とは違った角度から指摘していただけます。それが大変勉強になるのです。なぜなら,自分の中にはどうしても思い込みがあります。サークルに参加することで,思い込みを乗り越えさらにもう一歩レベルを上げていくことができます。

